燃焼室壁からの熱損失
|
|
|
|
|
| Heat Losses from the Wall |
|
|
エンジンの冷却 Cooling とはシリンダ内のガスから冷却剤への熱移動であって,エンジン工学のなかでひとつの分野を形成する.往復ピストン式エンジンでは燃焼室を構成する壁があり,その力学強度を維持し,壁表面の潤滑油温度をそれが潤滑油として機能する範囲内に保つために,冷却は不可欠である.潤滑油が機能する温度範囲に保てば壁材料の強度も維持され,導入新気の熱膨張もほどほどに収まるから,冷却の主旨は後者であるとも言える.扱う熱量は燃料が持っていた化学エネルギーの 20 - 50 % にも達するのであるが,たいていはそのほとんどをそのまま外気へ捨てる.熱機関である以上,低熱源に捨てるべき熱量 Q2 が存在することは必須であり,避けることは原理上できないが,低熱源に捨てるべき熱量 Q2 は基本的には排気で持ち去られるものであって,冷却 Cooling とは直接には関係しない.そのような意味で,エンジン冷却 Cooling はエンジンのサイクルとしては無くて差し支えない.
|
シリンダ内チャージの持つ熱エネルギーはまず壁のガス側に対流熱伝達 Convective Heat Transfer で伝えられ,固体壁内部を熱伝導 Heat Conduction で移動して壁の冷却剤側に達し,そこから再び対流熱伝達で冷却剤へ伝えられる.この様子を右図に示す.ガス側の熱伝達率を h [W/(m2⋅K)],壁の厚さを δwall [m],壁材質の熱伝導度を λw [W/(m⋅K)],冷却剤側の熱伝達率を hcoolant [W/(m2⋅K)] とすると,シリンダ内チャージから冷却剤への熱流束  [W/m2] は伝熱面積を AW [m2] として, [W/m2] は伝熱面積を AW [m2] として,

ここに K は熱通過率,熱貫流率 Overall Heat Transmission Coefficient [W/(m2⋅K)] と呼ばれる熱伝達の指標である.Overall を付けない場合もしばしばであるが,それだと,熱伝達率 Heat Transfer Coefficient h [W/(m2⋅K)] と紛らわしい.
|
|
|
温度勾配が小さいところは熱が移動し易いことを表している.熱伝達を評価するというのは温度勾配を知ることである.上の 1/K の式は熱移動のし難さの和という表現である.ガス側熱伝達率 h は通常,冷却剤側熱伝達率 hcoolant より一桁小さく,ここが熱移動抵抗として最も大きくて,シリンダ内チャージから冷却剤への熱移動はガス側熱伝達率 h がほぼ律速する.
このようにエンジンの冷却 Cooling ではチャージと燃焼室内側壁とのあいだの熱伝達が最も重要であり,冷却剤側の熱伝達がそれに次ぐ.それゆえ,以下の取り扱いのように,シリンダ内チャージから冷却剤への熱流束  として扱わず,チャージから燃焼室壁面への熱流束
として扱わず,チャージから燃焼室壁面への熱流束  を扱うことが多い.もっとも,冷却剤側熱伝達が先に問題になる場合も時に無くはなく,特に空冷ではしばしばそこが熱移動抵抗として最も大きくなる.水冷 の場合にはノッキングが起こった場合などを除き,ほとんど問題になることはない.
を扱うことが多い.もっとも,冷却剤側熱伝達が先に問題になる場合も時に無くはなく,特に空冷ではしばしばそこが熱移動抵抗として最も大きくなる.水冷 の場合にはノッキングが起こった場合などを除き,ほとんど問題になることはない.
シリンダチャージから燃焼室壁面へと逃げる熱量をどのように評価するべきかというのはなかなか難しい問題である.定常運転での熱負荷が分かればよいのか,それとも,どのクランク角で,燃焼室のどの部位にどう熱が伝わるのかというところまで知りたいのか,などによって,どう対処するかが変わるが,皆が納得するという方法はどこにもない.
1) 熱伝達実験式を使う,2) 多次元モデルを使った数値計算,3) 実測する,などである.1) 実験式 は簡便であるが,それでよいという保証はほとんどない.2) 多次元モデルは シリンダ内火炎伝播のシミュレーション の最終段階を取り出したものである.この取り扱いでは,壁に近づいた火炎の振る舞いと,火炎の 消炎距離 とが深く関係する.複雑であり,まだ途上段階に留まる.3) 実測 はそうそういつもどこでもできることではない.
1) Nusselt, Eichelberg, Woschni, Annand, Van Tyen など,いくつか実験式が提案されているのでそれを使う.これらの実験式では熱伝達率が平均ピストン速度,圧力,温度の関数として与えられる.燃焼室壁からの伝熱速度を次の定常熱伝達と同様に,h: 熱伝達率 [W/(m2⋅K)],AWg: 燃焼室壁伝熱面積 [m2],(Tg -TWg): シリンダ内ガス温度と燃焼室壁面温度との差 [K] の積として,

実験式は熱伝達率のそれが与えられ,例えば,Eichelberg の式は,

ここに,Cm: 平均ピストン速度 [m/s], p: シリンダ内圧力 [MPa] である.
対流熱伝達と輻射熱伝達とを分けて表示する場合もあり,それぞれを hconv, hrad とする.なお,Eichelberg の式では対流熱伝達と輻射熱伝達とは分けられていない.
この方法は簡便であるが,チャージの流動,乱れの効果をまずは平均ピストン速度 Cm でしか効かせられないから,そうしたものによる熱伝達の差異を考えようとするときには使えない.また,チャージの温度を何らかの方法で別途既知としなければならないが,これをどうして得るかが新たな問題になる.もちろん,燃焼室の場所場所で熱伝達挙動が局所的に違うことなどは最初から考慮に入っていない.さらに,定常的な熱伝達式を基にしているから,圧縮や膨張の効果,つまり,温度境界層が圧縮で薄くなるとか,それに時間遅れがあるというような,動的な効果というものも圧力 p の効果以外には表現されていない.
|
実験式の成り立ちが大型舶用ディーゼル機関のためのものであったこともあり,小型高速機関では絶対値が大きく異なるとも言われている.
右図は,行程容積 125 cm3 の 4 ストローク火花点火機関を 6000 rpm で運転したときの熱流束計測値を Eichelberg 式と比較したものである.Eichelberg 式の係数,上掲の 7.67 を 12.0 に置き換えて,シリンダ壁からの熱損失量が圧縮・膨張行程において合計で合致するようにしてある.熱流束のピーク値やその位相が大きくずれている.係数の問題を含め,これを使えると見るか,使えないと見るかは立場に依存する.
シリンダ内ガス温度 Tg について,チャージを空気と看做し,ガス法則,状態式で次のように算出する場合が多い.

|
|
|
希薄運転のディーゼル機関でならこれでもそれなりの合理性があろうが,量論混合気の火花点火機関についても,シリンダ内ガス温度 Tg をこれで与えている例を多く見受ける.学問から離れていると指摘しておく.せめて,Two-Zone Model で未燃混合気と既燃ガスに分け,どの壁のどこにどちらが接触しているかを見分けながら進めるべきであろう.そうでないと温度評価誤差はすべて熱伝達率のなかに詰め込まれるので,その物理的な意味が失われる.
|
2) シリンダチャージの流動を解き,数値計算で場の状況を知って熱損失速度を出そうとするもの.非定常の効果,つまり,圧縮や膨張の効果が記述されているのを期待するが,多くはそうでない.
・温度境界層の伸び縮み
燃焼のない乱流場で圧縮と膨張がなされる場合について,次式のような一次元エネルギー式で,右図のような配置を考えて,シリンダ軸方向に一次元温度分布を導いた例がある*.

 であり,全体に定圧比熱 cp を乗じ,それが単位容積あたりの量になっていると考えるとエンタルピ保存式であることが判る.εe は層流拡散係数と乱流拡散係数の和である.ピストンの動きによって右辺第二項の圧力仕事がシリンダチャージに付与される.これで壁近傍に温度境界層ができ,右辺第一項の乱流拡散が混合効果を与える. であり,全体に定圧比熱 cp を乗じ,それが単位容積あたりの量になっていると考えるとエンタルピ保存式であることが判る.εe は層流拡散係数と乱流拡散係数の和である.ピストンの動きによって右辺第二項の圧力仕事がシリンダチャージに付与される.これで壁近傍に温度境界層ができ,右辺第一項の乱流拡散が混合効果を与える.
|
|
|
|
下図はその計算結果である.T*=T/T0 である.横軸はラグランジュ的な位置を表し,Z=0 が壁,Z=1 がチャージの中央部である.この図表示ではピストンがチャージを圧縮しても温度勾配 ∂T*/∂Z はほとんど変化していないが,オイラー表現での実際の温度勾配 ∂T*/∂x は ∂T*/∂Z に ρ/ρ0 を乗じたものであるから,圧縮中刻々温度境界層が壁に押し付けられて縮む.
いま仮想的に,ピストン圧縮を -30o で止め,温度,圧力,流れなどをそのときの Z=1 の条件に保って放置すると,上式,右辺第一項の乱流拡散が効いて,温度分布は一点鎖線の壁法則温度へと収束する.この差異が圧力仕事の効果であって,ピストンエンジンでは常にこれがある.圧縮による温度上昇は熱拡散より速いという意味である.
膨張行程に入ったあと,60o, 90o の温度分布を見ると,中心部のガス温が壁温より高いのに,壁近傍の温度勾配は負で,熱は壁から中心部に向かって流れる.これについても,ピストン膨張による温度降下に対して熱拡散が遅れることがその理由である.
こういうふうに見て行くと,熱伝達率 h の実験式のもとになっている,先に挙げた次の関係では,温度境界層が伸びたり縮んだりする効果も熱伝達率 h のなかに埋め込まれているから,定常状態でなければ物理的な意味を持たないのではないかと訝られる.

|
|
|
* Nishiwaki, K., "Multidimentional Modeling of Flow and Heat Transfer in Engine Cylinders", 11th National Conference on I. C. Engines and Combustion (1989), 1-19 ならびに 西脇一宇,エンジンの伝熱,自動車技術 59-4 (2005), 120-123.
・多次元流動・熱伝達計算
これを多次元に拡張し,燃焼も入れてシミュレートしようとする試みがいくらかなされている.基礎式は前掲のエンタルピ保存式に熱発生項を追加し,次元を増やして次式のようになる.ここに,Mf: 燃料の分子量 [kg/mol],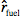 : 燃料が消費される速度 [mol/(m³⋅s)],hc: 発熱量 [J/kg] である.
: 燃料が消費される速度 [mol/(m³⋅s)],hc: 発熱量 [J/kg] である.

多次元モデルでは,上に示したような圧力仕事の効果を考慮している例はなく,境界層温度分布は壁法則で処理されている.熱伝達が興味の対象になっているとはいえ,これは シリンダ内燃焼過程のシミュレーション そのものである.
|
パンケーキ型燃焼室において,15°bTDC にて中心点火されて伝播する火炎が燃焼室端に近づく挙動とそこでの熱流束を,幾つかの計算手法で比較した例* がある.量論混合気で,圧縮比は 7.2,回転速度 750 rpm である.その結果を右図に示す.
計算手法 a) HFFM は Hybrid Fractal Flame Model と称されるもので,考え方は火炎伝播シミュレーションのページで述べた CFM に類似のものである.b) Weller とあるのは論文** の著者名で,手法は G-Equation によっている.c) HFFM-cl は HFFM で確率密度で扱っているところを反応進行度に替えた手法である.
図の左列が反応進行度,左列が局所熱発生率の計算結果であり,上死点後 10°の状況が表示されている.いずれのモデルでも,圧力経過や熱発生経過は,実測値を模擬しており,優劣つけがたいという.乱流火炎のスポンジ状領域 Flame Brush 厚さもほぼ再現されている.
この三つのモデルで計算された熱流束の代表値は下図のようであり,シリンダ半径の 2/3 にあたるシリンダヘッド面における値である.熱流束は火炎の到来とともに急速に立ち上がった後に緩むので,その経過にはっきりした折れ曲がりが見られる.HFFM ではこの傾向は比較的弱く,壁消炎モデルを組み込まなくてもその経緯は変わらないとされている.実測の熱流速経緯にはこうした折れ曲がりは見られない.
|
|
|
|
火炎帯形状と熱流束はモデルに依存しており,火炎と壁との干渉を充分に表現できる段階に達していない.特に c) HFFM-cl では,火炎面形状が進行方向に凹で不自然である.シリンダ内燃焼過程シミュレーションにおいても,その最終段階である壁近傍の挙動は解き明かされているとは言えないと知れる.もっとも,詳しい実験結果も不足している.
こうした取り扱いでは,壁に近づいた火炎の振る舞いとも関係するので,消炎挙動 とのかかわりも興味の対象になる.ピストンエンジンにおける燃焼室壁からの熱伝達は重要なテーマであるし,周辺技術はこの手法の発展を可能にしつつあると思われるのに,まだあまり進展していない.これを専門的に取り扱っている研究者が少ないのが残念である.壁付近の流動/乱れと火炎との干渉をモデル化する段階でいまだ大きな進展がみられない.西脇一宇先生によると,ここに示したように,現段階の燃焼時熱伝達予測計算では実際の現象と,特に壁面熱流束履歴と,いまだかなり乖離しているとのことである.
|
|
|
* Nishiwaki, K., "Modeling Engine Heat Transfer and Flame-Wall Interaction", 4th COMODIA, (1998), 35-44 ならびに 西脇一宇,エンジン熱伝達および火炎の壁面干渉関するモデリング,エンジンテクノロジー 1-1 (1999), 26-33.
** Weller, H. G., Uslu, S., Gosman, A. D., Maly, R. R., Herweg, R. and Heel, B., "Prediction of Combustion in Homogeneous-Charge Spark-Ignition Engine", 3rd COMODIA (1994), 163-168.
3) 実測するもの.時間ができ次第,以下に実測値の例を挙げて説明しようと思う.実測には手間と費用がかかるうえ,実機と同一条件で計測するのはかなり難しい.Know-How の蓄積も要る.もちろん燃焼室のどの部位でも測れるというわけではない.
・実測手法の一例
以下は 1970 年代末にやっていた仕事* の一部であり,実機の熱損失を知るという動機はからなされたものではなく,ピストン圧縮予混合自着火における圧力依存性を調べる手法として進めたものである.動機は違えども,考え方が違うわけではなく,手法としては同様であると考えられるので,ここに掲載する.
* Ohta, Y. and Takahashi, H., "Temperature and Pressure Effects in Cool and Blue Flames", Flames, Lasers and reactive Systems, Vol. 88 of Progress in Astronautics and Aeronautics (1983), 38-56, AIAA.
実測といっても,熱流束それ自体が観測量というものはない.表面温度履歴の計測データから,壁の奥行方向に半無限固体と仮定した熱伝導計算をするのが通例である.表面はあくまでも表面であって,固体のそれであるとはいえ,空間分解能は充分高くなくてはならない.つまり,表面の極々薄いところの温度履歴を得る必要がある.
・表面熱電対
壁の奥行方向に,隔たった二箇所の温度が測れると,かなり直裁的に熱流束を知ることができる.もちろん,このときでも温度測定部の空間分解能が要求され,極々薄いところの温度が得られて初めて可能になる.そういう熱流束センサが市販されたこともあるようであるが,詳しいことは知らない.
壁表面温度測定用の表面熱電対の仕様を右図に示す.鋳鉄円筒を二つ割りにし,その間に銅とコンスタンタンの薄板をテフロン膜を絶縁材にして挟み込んである.図右下に示すように,燃焼室壁となる部位に熱電対素材の端面が現れるから,そこに T (CC) 熱電対の高温側接点を銅鍍金で構成する.銅鍍金はシアン化銅溶液を使った電気鍍金という古典的な方法に依っている.銅鍍金の厚みは,鍍金浴に浸けて通電している時間で設定し,供試したものではおよそ 3 µm である.
|
|
|
|
銅鍍金するということは,熱電対の高温側接点を構成するという意味の他に,鍍金面の奥行き方向だけではなく,面拡がり方向の熱伝導の良さで,熱電対高温側接点情報を鋳鉄表面本来の温度情報に近づけようとの意図を含んでいる.
燃焼室のシリンダヘッドは右図のようになっていて,母材は鋳鉄である.単サイクル圧縮自着火を起こす装置なので,ポペット弁はひとつで済む.このシリンダヘッド,赤色のところに前図の表面熱電対が面一 (つらいち) になるように嵌め込まれる.弁を除いて,燃焼室壁をすべて同質の材料とするため,ピストン頂面に鋳鉄製円板を貼付けた.これで燃焼室形状は完全なパンケーキ型になっている.実機ではこういう単純化はできないけれども,現象を見るために用意されたピストンエンジン-like な装置では,こうした単純化が計測精度の向上と現象の普遍性をもたらす.燃焼室壁材を同質とするのは,一箇所で測った熱流束を,他の部位でもそれであると看做したいがためである.
|
|
|
壁表面温度測定用表面熱電対では,その母材を周辺のそれと同一に揃えることが肝要である.市販の熱流束計* ではここを揃えられないのが難である.* 例えば Medtherm TCS-102-E など.
・熱流束 Heat Flux を求める
燃焼室壁からどれだけ熱が逃げるかを表すには,その速さを次のように,熱流束 Heat Flux  [W/m2] と伝熱面積 AW [m2] の積として,熱流束として取り扱うのが便利である. [W/m2] と伝熱面積 AW [m2] の積として,熱流束として取り扱うのが便利である.

固体表面 x = 0 における熱流束  は,そこでの温度勾配と固体の熱伝導度 λw とから, は,そこでの温度勾配と固体の熱伝導度 λw とから,

ここに,x は固体表面からの深さ,θ はそこの温度である.
|
|
|
半無限固体とは x = 0 から x= ∞ まで拡がっている固体であり,熱は x = 0 の面に垂直方向に流れるとする.初温度が x のみの関数 θ = f(x) であって,表面 x = 0 で温度を 0 としたとき,熱伝導方程式は,

ここに,αw は温度伝導度 or 熱拡散率 Thermal Diffusivity [m²/s], αw = λw/(c⋅ρ),c: 比熱,ρ: 密度,t: 時間である.
展開はここから出発する.一般にはフーリエ級数で表現する手法が採られるようであるが,ここでは折線近似法を先に紹介する.
初温度が T0 で,ある時刻の表面温度が TW のとき,時間 t に対して j を定数として, なる直線変化であるなら,表面 x = 0 では, なる直線変化であるなら,表面 x = 0 では,

という関係になる.そのとき熱流束は,

そこで,測定された表面温度履歴 TW を上図のように n 個の折線で近似し,それぞれ線分の時間に対する勾配を jn としたとき,重ね合わせの方法により,熱流束は次のように表される.

|
|
|
この折線近似法について,詳しくは,川下研介,熱伝導論,(1966), 72, オーム社 に出ている.式の展開をフォローするのは骨が折れたが,院生ともども,複数人で確認してある.単サイクルの経緯から熱流束を出すにはこちらの方がフーリエ級数表現にするより問題が少ない.フーリエ級数表現は交流的といおうか,変動を均した時間平均値から出発する必要があるからである.
上に挙げた図は,上述した,ピストン圧縮予混合自着火における圧力依存性を調べたときの計測例である.昔のことで,データ採取はアナログ式,ブラウン管オシロスコープを使って撮ったものである.混合気はエチルエーテル/空気,当量比 0.5 である.壁温の変化は僅かに 2-3 deg K で,インピーダンスは低いとはいえ,熱電対出力は微弱であり,千倍に増幅して記録されている.当時,最も低ノイズと言われた National Semiconductors: LH0044 という OP アンプを使った.通常のエンジンでなら壁面温度振幅は十度から数十度ある.この結果の説明は別途 "低温度自着火講義" の中の "圧力依存性" のページで.
 Still not fixed !
Still not fixed !
|
�「言わずもがなのことだが,内容の一部であろうとも 無断転載を禁ず�」
引用する場合にはこのページもしくはこの Web site の所在を明記されたい
Copyright © 1995-2016, Y. Ohta, All rights reserved. Except as otherwise permitted by written agreement, the following are prohibited: copying substantial portions or the entirety of the work in machine readable form, making multiple printouts thereof, and other uses of the work inconsistent with Japan and applicable foreign copyright and related laws.
|
![]() [W/m2] は伝熱面積を AW [m2] として,
[W/m2] は伝熱面積を AW [m2] として,










 Still not fixed !
Still not fixed !