これについては専門ではないので詳しくはなく，以下の記述はとおり一遍の域を出るところはない．しかし，エンジンのシリンダ内燃焼を考える上で避けて通れない．1970 年代後半で研究が終わっているようにも見えるが，すっきりと説明がなされているわけではない．燃焼室壁からの熱損失を考える上でも欠かせない．シリンダ内ガソリン直接噴射としたとき，このあたりがどう変わるかということも興味ある事項である．内燃機関周辺の研究者・技術者で，あるいは一般の人でも，このページを読もうとお考えになった方なら，こうしたことがなぜ基本的な事柄であるかを理解なさるに違いない．

　火炎帯厚さ Flame Thickness，消炎距離 Quenching Distance，最小点火エネルギー Minimum Ignition Energy，可燃限界 Flammability Limits は火炎の成立ということから言えばひとつの事項である．それゆえ，互いに関係しあっていて，独立の物性値ではないが，目的が異なっていたり，視点が別々であったりして，それぞれ単独に測定されている．測定値は実験装置・手法に大きく依存し，データ間での差が大きく，相互に明確に関係づけられた包括的で整合のとれたデータはまだない．

　混合気中を火炎が伝播するとき，火炎が固体壁に近づくと，壁に熱を奪われて，ある距離以下にまでは近づけず，そこで 消炎 Extinction が起こる．壁近傍の，この火炎伝播が阻害される領域の厚みを消炎距離 Quenching Distance という．細い管のなかを火炎が伝播するとき，あるいは平行平板間の狭い隙間を火炎が伝播するとき，管径や平板間隔がある閾値以下に小さくなると，伝播しなくなる．これらは，最小火炎伝播直径 d_q，最小火炎伝播平板間隔 δ_q2 というように細分化される．最小火炎伝播直径, d_q や最小火炎伝播平板間隔, δ_q2 は Head-on Quenching Distance, δ_q1 に較べれば測定が容易であってデータも多くある．しかしこれらとて，大気圧下のデータがほとんどで，高圧でのデータは少ない．この現象においては，層流底層で起こるものであるから，混合気流動や乱れの影響は考える必要がない．

　なお，テールパイプへの Hydrocarbon, HC 排出量はこの消炎距離とは直接には関係しない．火炎伝播の終段でシリンダ壁に HC が残る機構はこの消炎距離によるものであるが，それは排気行程で掻き取られると同時にかなり酸化されるので，実際の排出量はずっと下がる．予混合火花点火機関の燃焼効率が 0.97 程度であるということの方が消炎距離が関係する重要事項である．

・ 平行ニ平板消炎距離　Two-Plate Quenching Distance，δ_q2

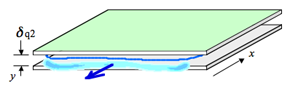
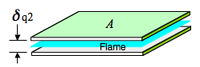
平行ニ平板のあいだに置かれた混合気中を火炎が伝播することを考えると右図のようである．このとき，間隔を狭めて行くと火炎がその隙間を通り抜けることができなくなる．この現象は火事が発生したときに延焼を防ぐというような，安全工学の面で重要である． 　伝播するかしないかぎりぎりのとき，隙間内でどのようなことになっているのかを実験で詳細に見るのは難しい．数値計算で現象のあらましを押さえた例* をここに挙げる．

二次元火炎伝播計算の初期のもので，化学反応は一本の一次反応アレニウス式で与えられる．右図は消炎限界での計算結果で，平行平板間隔は 2.56 mm である．反応は一次反応，Lewis 数は 1 であるとしたときのもので，大気圧下での量論の プロパン C3H8/空気 混合気が想定されている．壁ならびに混合気の初温度は 300 K である．比熱，熱伝導度はともに一定値としている． 　縦軸 y の 0 位置が壁であり，y=1.28 mm のところが隙間の中央である．横軸 x 方向のこの中央では先のページに示した層流火炎伝播の予熱帯から反応帯に至る経緯が実現されている．もっとも，断熱系でなら既燃ガスは明確な熱源であるのに，ここでは非断熱なので既燃ガスはどんどん冷えて行き，後方支援の無い火炎 になる．おそらくx=5.0 mm では 2000 K 以上の部分はほとんど無いであろう．火炎背後の高温既燃ガスがわずか 2 mm うしろではすでに高温とは言えなくなる．全体が冷やされている伝播火炎 である．

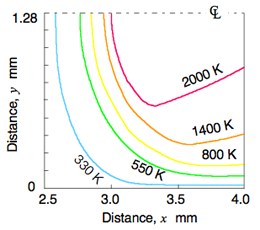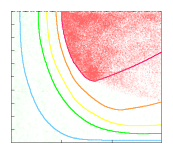
2000 K に達した部位 (赤線の内側) は燃えたと看做せようから，x=3.3 mm あたりで，中央部だけ，ほぼ半分の混合気が燃えたということになる．x=3.3 mm より後方，x の大きいところでは既燃ガスはどんどん冷やされ，あわせて壁に近いところの未燃ガスと混ざる．そこでは赤線の内側だけが既燃ガスであるわけではない．既燃ガスを赤点の集合で表現して，推量でその様子を描くと右図のようになろうか．このページ一枚目の図はこうしたことを踏まえたもので，手前の薄青い，やや拡がった火炎は，平行二平板の拘束を解かれて，大きくなろうとしている火炎を想像してのものである． 　火炎幅がどんどん小さくなって，ごくごく小さい火炎で消炎限界に至るという現象ではないことに留意されたい．

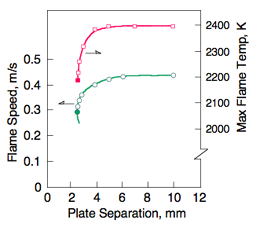
最高到達火炎温度は 2180 K とのことなので，2000 K に達したところを燃えたと考えるにしろ，発熱の最後まで行かないところも多かろうから，これで全体としての燃焼効率は 0.5 に達しないと思われる． 　平行ニ平板の間隔によって，最高到達火炎温度や火炎速度がどう変わるかを示したものが右図である．隙間が 6 mm 以上あれば，中央部分に断熱に近い領域があって，わずかながら膨張による加速も観察される．断熱層流燃焼速度 SL = 0.41 m/s に対して火炎速度は 0.44 m/s になっている．隙間が小さくなると，到達火炎温度と火炎速度がともに低下して，壁への熱損失が効いた状況下で，かろうじて火炎伝播が維持されている状態になる．極限では隙間を減らす効果が無限大となる様子が左図に表現されている．このときの 2180 K, 0.28 m/s という値がどういう物理・化学的意味を持つかを考えてみるべきであろう．

・ 消炎を考えるときの基本概念：ペクレ Peclet 数

　火炎の熱発生と壁への熱損失との比はペクレ Peclet 数と呼ばれ，消炎限界は発熱速度と熱放散速度が等しいところであると考える；これが基本で，この論理から行くとペクレ Peclet 数は 1 であるはずのところ，実際には，消炎限界 Peclet 数は 1 よりはるかに大きい．しかしながら，おおよそは定数とみなしてよいと言われている．
　平行ニ平板について，火炎伝播による熱発生速度は であり，壁への熱伝導は である．ここに A_f, A_w はそれぞれ火炎面積，壁の面積である．添字 f, u はそれぞれ，火炎，未燃混合気 (壁) を意味する．平行ニ平板について，火炎面積，壁面積を等しいとして，Peclet 数は，

で定義される．上図のように，隙間全体に火炎が存在すると言う想定，あるいは一次元での考えに基づいているのであろう．

　しかし，平行ニ平板についてここで問題なのは，上記数値計算でも示されるように，温度 T_f である火炎面積は壁の面積に較べて圧倒的に小さい．消炎限界 Peclet 数が 1 よりはるかに大きいのはひとえにこれによる．この場合，一次元性は担保されず，二次元での取り扱いでなければ記述しえない．むしろ，次に述べる Single Wall, Head-on Quenching Distance についてなら，火炎面積と壁面積が異なるという問題は生じない．

　また，別途問題になるのは，比熱 c_p や熱伝導度 λ に物質・温度依存性があることであり，未燃混合気 (u) を採るのか，火炎温度の既燃ガス (f) を採るのかで値が大きく変わってしまう．それにしても，ペクレ Peclet 数を定数とみなし得るなら，場の温度や圧力が上がったときにどうなるかを評価することができて有用である．ペクレ Peclet 数が定数であるというのは，温度，圧力，当量比などが変化しても，伝熱関連の配置 Configulation はほぼ同じで変わらないという意味であろうか．

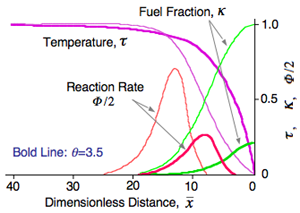
・ 接近消炎距離　Head-on Quenching Distance，δq1 　Single-Wall Quenching Distance とも呼ばれる．火花点火機関のシリンダ内火炎伝播のように，火炎が壁に向かって伝播して行き，壁にあたる直前に消えるときの Head-on Quenching Distance, δq1，接近消炎距離ともいうべき値は，燃焼完結度合，燃焼効率，Hydrocarbon, HC 排出量などの観点から重要である．しかし，この距離を測定するのはかなり難しく，データは多くない． 　先の平行ニ平板の場合と異なり，一次元の取り扱いで問題ない．ここではその解析例* を紹介する．比熱は一定値ながら，熱伝導度は温度に比例すると扱っている．値はすべて無次元数になっている．ルイス Lewis 数は 1，無次元活性化エネルギー のときのものである．下左の図が空間配置で，細線が壁から遠い火炎，太線が壁に近い火炎で、消炎限界相当する時期のものである．火炎が壁から離れているときには，壁近傍の温度勾配は比較的ゆるやかであるが，火炎が壁に近づいたときには，当然のことながら，温度勾配は急峻になり，反応帯，既燃ガスは激しく冷やされる．

　Head-on Quenching では非断熱ながら，火炎背後の高温既燃ガスは断熱系と同じように，後方から火炎を支援する熱源となっている．ルイス Lewis 数を 1 としているから，壁面の燃料も動いて，壁面燃料濃度はかなり低くなっている．ここでの無次元距離はペクレ数と同じものである．
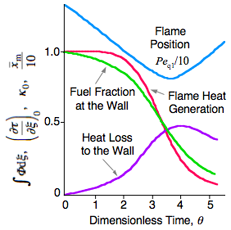
　上右の図が，火炎が壁に接近するときの時間経過であり，熱発生と熱損失のせめぎ合いが示されている．火炎は消炎限界距離まで近づいたあと後退し，ペクレ数は極値を取るというところが興味深い．

　解析から得られた整理は上右の図からも分かるように， ということである．このペクレ数は "Kaskan 大気圧下プロパンについての実測値: 0.28 mm" を入れると良い一致を示すが，この解析から得られる Head-on Quenching Distance, δ_q1 の値は、エンジンシリンダの実験値よりはるかに小さく，数分の一であるという．圧力依存性が表現できていないらしい．

　*Kurkov, A. P. and Mirsky, W., An Analysis of the Mechanism of Flame Extinction by a Cold Wall, 12th Symposium (International) on Combustion, (1968), 615-624

　2007 年になって，これと同じ Single-Wall Head-on Quenching について，Purdue University の Rebecca Owston という人が化学種を含めた計算をし，その結果が Combustion & Flame に発表されている．現象としては上記のものと寸分違わない．ここ 40 年間の進歩とは何であるかを反芻するとともに，昔の人の力量というものに思いを馳せた．

　Head-on Quenching Distance, δ_q1 を高圧下を含めて計測した比較的最近の例** として次のものを挙げておく．
量論のメタン-空気層流火炎について，

Pressure Range: 　　　 　0.05 to 1.7 MPa
Quenching Distance: 　 　0.43 to 0.016 mm
Maximum Wall Heat Flux: 0.35 to 2.3 MW/m²

火炎が壁近傍の温度境界層と干渉する時間は圧力にかかわらず 0.15 - 0.155 ms とほぼ一定であるという．

　** Sotton, J, Boust, B., Labuda, S. & Bellenoue, M., Head-On Quenching of Transient Laminar Flame: Heat Flux and Quenching Distance Measurements, Combustion Science and Technology, 177-7, (2005), 1305-1322

　メタン CH₄ はガソリンから見るとかなり性質の異なる燃料であるから，そのデータの解釈には注意を要する．プロパン C₃H₈ の方がまだしもガソリンに近い．

・ 消炎距離についての諸量間の関係

　Lavoie, G. A. は消炎距離について，過去に得られているデータをレヴュし，半理論/半実験式を導き，併せて平行ニ平板消炎距離 δ_q2 と Head-on Quenching Distance, δ_q1 との関係，消炎直径 d_q との関係を与えている*．

　未燃混合気の初期温度で物性値を与えたときの消炎限界 Peclet 数，Pe_n,u (ここに，添字 u は比熱 c_p と熱伝導度 λ に未燃混合気の物性値を与えたことを意味する)

これらはすべて，1978 年の Lavoie の論文以前に出版されていたデータを整理して得られたものである．どの範囲でどの程度あてはまるのかははっきりせず，概略これくらいというように考えておいた方が安全である．

　いま，反応が可能な混合気容積と壁の面積との比で，平行ニ平板消炎距離の円管等価直径を考えるなら，円断面では面積/接触周長さは なので，これになぞらえて，4×面積/接触稜線長さを等価直径とすると， であるから， となるはずであるが，ここでは比例定数は 0.5 でなく，0.65 になっている．混合気容積全体が発熱するわけではないことに依るから，一筋縄では行かない．　

　*Lavoie, G. A., Corelations of Combustion Data for S. I. Engine Calculations - Laminar Flame Speed, Quench Distance and Global Reaction Rates, SAE Paper 780229

・ 消炎距離を考えるときの基礎式

　消炎を取り扱う場合にも，一次元層流定常火炎 の質量，化学種，エネルギーの保存式が成り立つから，それを現象に合わせて少し拡張すればよい．

　定常状態でなく，非定常なら，

のように，時間変化項を足す必要がある．上で，Head-on Quenching を扱ったときには，これが基礎式になっている．ここに，M_f: 燃料の分子量 [kg/mol]，: 燃料が消費される速度 [mol/(m³⋅s)]，h_c: 発熱量 [J/kg] である．

　定常ではあるが，一次元では済まぬときには，熱伝導項を二次元に拡張し，

とする．二平板間での消炎距離の取り扱いではこれがもとになっている．

　燃料が消費される速度は，アレニウス形で，

のような一本の式で，不可逆反応として扱われることが多い．b は Pre-exponential Factor である．

　こうした消炎距離の取扱いは，以降の進展も加えて，

Ezekoye, O. A., and Greif, R., "A Comparison of One and Two Dimensional Flame Quenching: Heat Transfer Results", (1993), Lawrence Berkeley Laboratory, LBL-33817, UC-310

に纏められ，Internet 上に pdf ファイルで公開されている．Lewis 数の影響を含め，エネルギー保存のモデル化手法が比較的よく説明されており，一見の価値あり．上掲の二例はこの仕事より時代を遡った，昔のものであるが，内容の本質に変わりはなく，ここの引用文献にもなっている．これらには，独自性とともに，表現に見るべきものがある．

・ 壁乱流が火炎に干渉するときには

　消炎距離についてはまずは層流火炎を取り扱えばよいはずで，それには壁近傍に層流底層が存在するという意味が大きい．しかし，流れが乱流で，火炎も乱流火炎であるとき，この現象がどのように変わるのか，あるいは変わらないのかを把握しておく必要がある．壁乱流と火炎との干渉をこの ｢消炎距離｣ のページに取り上げるのが適当かどうか，｢燃焼室壁からの熱損失｣ のページに置くべきものではないかと迷う．しかし，エンジンのシリンダ内燃焼で火炎が燃焼室壁に近づいたとき，その壁近傍がいわゆる壁乱流構造になっているのかどうか，そこをはっきりさせた人はまだいない．ピストン圧縮されたあとの燃焼期間中，燃焼室壁に平行な定常主流れが明確に存在するのかどうかということでもある．それゆえ，確実に壁乱流場が与えられたときの火炎と熱伝達とはどういうものかを考える，という意味でここへ置いた．

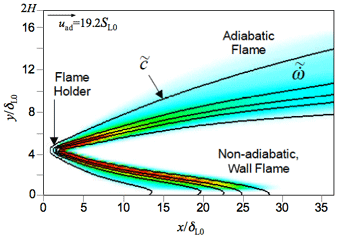
消炎距離を謳っていないが，University of Wisconsin-Madison の C. J. Rutland らが壁近傍での火炎挙動と熱流束を以前から DNS で計算している*． 　右図のような配置で，矩形断面のチャンネルに混合気が左から送られて来る．下面が壁で，上方は uw なる速度で動く断熱壁の，いわゆる Couette 流が想定される．流れ方向に x，高さ方向に y，幅方向に z 軸が採られ，チャンネルは y 方向に高さ 2H，z 方向に幅は無限大である．上側断熱移動壁速度 uad = 19.2SL0，チャンネル高さ 2H = 17.5δL0 という設定になっている．流れの Reynolds 数は H，平均流速 uad/2 について Re = 504 である．アプローチ流れにおける乱れは u' < SL0 であって，乱流火炎形態 はSingle Sheet，ゆるやかな皺火炎である． 　図中の は平均反応進行度で，実線で示され， は平均反応速度で，色表示である．壁は未燃混合気と同じ温度とおかれている．反応は一本のアレニウス式で与えられる．

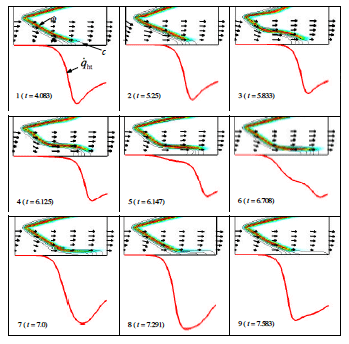
チャンネルに入ってすぐのところ，0.5H の高さに熱線のフレームホルダが水平，z 軸と平行に置かれて，そこから発達する火炎は，いわゆる V 形火炎であり，上方，断熱移動壁側に形成される火炎と，下方，固定壁側に生じて，壁に熱を取られる火炎とに分かれる．それらの内部は既燃ガスである．乱流場が設定され，アプローチ平均速度が uad/2 = 9.6SL0 と高く，層流火炎速度 SL0 よりはるかに大きいので，フレームホルダ無しでは火炎は吹き飛ぶ． 　乱流境界層が火炎と壁への熱流束に与える影響，あるいはまたその逆の影響はまずは右に示されるようなものであり，時間経過と共に火炎位置と熱流束 が刻々変動する．火炎における熱発生は局所流速を，ひいては平均流速を上げる．特に下方，壁に向かって発達する火炎への影響が大きく，火炎が壁に沿ってくるところあたりで大きな時計廻りの渦が生成されていることが見てとれる．壁で冷やされる状況が変動するので，反応速度が変化し，火炎の曲率が変わる．火炎が壁に近づいたときに熱流束が大きくなる．上方，断熱移動壁側火炎も渦の影響を受けて火炎位置が変動する．また，拡散も促進され，平均反応進行度 等高線の間隔が拡がる． 　右上の図においては，平均反応進行度 の勾配が壁近くで反転し，この渦によって火炎が壁に押し付けられる様子が表現されている．

壁への熱流束 を色分けで示したものが右図である．渦は幅 z 軸方向に伸びた円筒ではなく，三次元の，ぐにゃぐにゃした球のようなものであると知られる．主流流れ x 方向に熱流束の大小があるだけでなく，幅 z 軸方向にも大きく変動する．

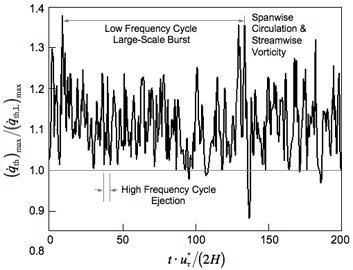
壁乱流 には壁近傍層に縦渦とストリーク Streak という 準秩序的な構造 があり，複数のヘアピン状縦渦が流れ方向に存在し，それらがまとまってパケット Packet と呼ばれる低速ストリークを構成する．ヘアピン渦の周囲にはイジェクション Ejection やスウィープ Sweep などの上向きや下向きのジェットが発生して，レイノルズ応力の発生原因となると共に，スウィープが当たる壁面では摩擦が増大する． 　乱流熱流束の最大値を層流熱流束の最大値との比で表したのが右図である．横軸の時間 t+ は Wall Friction Velocity 摩擦速度 [m/s] で正規化されていて，τw は壁面剪断応力 Shear Stress [N/m2=kg/(s2⋅m)] である． =0.727， =0.038 が設定値である． 　乱流になっても最大熱流束は平均的には層流の場合の十数パーセントの増に留まっている．

　壁乱流と干渉する下側の非断熱火炎はその縦渦とストリークという構造の影響を直接受けて，低速ストリークにおけるスウィープの効果で熱流束 が増大する．火炎は Reynolds Stress を増やし，これが熱流束 を増大させる．は流れ方向の大きい渦によってもたらされる下向きスウィープが寄与する．

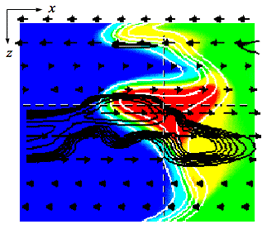
乱流境界層が熱流束 に与える効果を図示した一例が右図である．時刻 t+ = 32.85 のものである．二つ上の図と同じように，流れ方向 x - 幅方向 z なる冷却壁面における熱流束等高線が白の実線で表示され，局所熱流束の大きさが色で区別される．青，緑，黄，赤の順に局所熱流束が高くなる．ひとつ上の図で示された乱流熱流束最大値の層流熱流束最大値との比という尺度で，青は 0 に，赤は 1.4 に相当する．高さ y+ = 5 における平均流からの速度偏差 u' が速度ベクトルで表示され，低速・高速ストリークがそれで露になる．低速ストリークのある位置で熱流束 表示が黄色になっていて，そこで熱流束が増えていると知られる．黒の実線で表されるのは同じく高さ y+ = 5 における負のレイノルズ応力等高線である．流れ方向の渦が生じているところで熱流束 が赤もしくは黄になっていて，熱流束が著しく増大することが示されている． 　 はいわゆる Wall Unit [m] であり，ν は動粘度 [m2/s]，x+, y+, z+ は Wall Unit で正規化されたそれぞれの軸方向距離である．

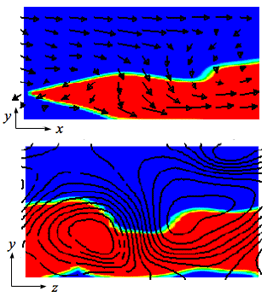
上図に縦・横の点線があるが，その断面で火炎がどうなっているかを示したものが右図である．上側には，上図横水平点線断面，流れ方向 x - 高さ方向 y なる面の，z+ = 79.6 位置における反応進行度 c の等高線が色分けで与えられている．赤が既燃ガス，火炎は黄から空色のところである．併せて描かれている矢印は平均流からの速度偏差のベクトルである．u', v'に対応する．チャンネル半値高さ H くらいのサイズを有する反時計方向回転渦が，上方断熱火炎を凹に歪ませ，同時に下方，非断熱火炎を冷却壁に押し付けている．この状況が二つ上の図にある Low Frequency Cycle なる時間間隔で生じる． 　下側は，上図縦垂直点線断面，幅方向 z - 高さ方向 y なる面の，x+ = 111 位置における反応進行度 c の等高線色分けである．赤が既燃ガス，火炎は黄から空色のところであるのは上側の図と変わらない．併せて描かれている黒い線はその面内の変動速度流線であり，平均流からの偏差 v', w'に対応する．渦は三次元的であり，そのサイズは上側の図と同等である．その渦サイズが，冷却壁に押し付けられている火炎がとそうでない火炎との間隔を決めている．

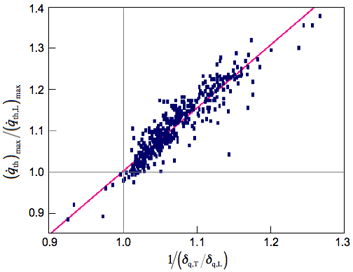
それでは，このページの表題である消炎距離 δq はどうかというと，右図のようである． 　縦軸は先の図で出た乱流熱流束の最大値と層流熱流束の最大値との比である．横軸の は乱流火炎における消炎距離 δq,T と層流火炎における消炎距離 δq,L との比の逆数であり，もちろん なのであるが，比較対象が層流における値なのでこう表現されている． 　まず，乱流熱流束が大きいときには消炎距離 δq,T は小さい．乱流熱流束と消炎距離とは逆比例の関係にある．これは流れと乱れの効果で一時的に火炎面が壁方向に押し付けられて熱流束が増加するという状況である．一瞬そこまで火炎が近づいたということの表現にすぎないから，これを消炎距離と言ってよいかどうかという疑問も生じるだろう．しかし，乱流場での消炎距離 δq,T を出せと言われれば，これしか無いのかもしれない．

　Alshaalan の学位論文が 1997 年に出て，その年，Combustion Science and Technology 誌に投稿されて，2002 年に掲載されている．変数の定義がはっきりせず，どういう物理量で正規化されているかというようなことが一読ではとても分からない．図も美しいとは言えず，かつ分かりにくい．ここに載せた図も已むを得ず描き直したり付け足したりしてある．スタートから何年も経過していて，これまで講演会などで数編の論文が発表されている．しかしそれらに見られる計算条件はここに挙げたものこれ唯一である．

　Still not fixed !